7.4. კუმულატიური ალბათობის ფუნქცია
ხშირად სასარგებლოა ალბათური განაწილება სხვა სახითაც წარმოვადგინოთ. რაიმე \( X \) დისკრეტული შემთხვევითი ცვლადისთვის კუმულატიური ალბათობის ფუნქცია, \( F(x) \), გამოსახავს ალბათობას იმისა, რომ \( X \) ნაკლებია ან ტოლია \( x \)-ისა, ანუ: $$ F(x)=P(X≤x) $$ სადაც \( F \) ნებისმიერ \( x \)-ში განსაზღვრული ფუნქციაა. მაგალითად, მონეტის ორჯერ აგდების ექსპერიმენტის შემთხვევაში კუმულატიური ალბათობის […]
7.3. ალბათობის ფუნქციის თვისებები
დავუშვათ, \( X \) წარმოადგენს რაიმე შემთხვევით დისკრეტულ ცვლადს ალბათობის ფუნქციით \( f(x) \). მაშინ ფუნქციას გააჩნია შემდეგი 2 თვისება: 1. ნებისმიერი \( x \)-თვის სამართლიანია: $$ 0≤f(x)≤1 $$ 2. ყველა ცალკეული შედეგის ალბათობათა ჯამი 1-ის ტოლია: $$ \sum_{x} {f(x)}=1 $$ პირველი თვისება ფაქტიურად აღნიშნავს ჩვენთვის კარგად ნაცნობ ფაქტს იმის შესახებ, რომ ალბათობა შეუძლებელია იყოს […]
7.2. დისკრეტული შემთხვევითი ცვლადის ალბათური განაწილება
დავუშვათ, \( X \)-ით აღნიშნულია რაიმე შემთხვევითი ცვლადი, ხოლო \( x \)-ით კი – მისი შესაძლო მნიშვნელობები. საზოგადოდ, იმ ალბათობის აღწერას, რომლითაც \( X \) იღებს \( x \) მნიშვნელობებს, ეწოდება ამ ცვლადის ალბათური განაწილება. ალბათური განაწილების ალგებრულად აღსაწერად დისკრეტული შემთხვევითი ცვლადისთვის განიმარტება ალბათობის ფუნქცია, ხოლო უწყვეტისთვის კი – ალბათური სიმკვრივის ფუნქცია (რომელსაც მომავალ თავში […]
7.1. შემთხვევითი ცვლადის ცნება
როდესაც შემთხვევითი ექსპერიმენტის შედეგები რაოდენობრივი სიდიდეებია, ალბათობის გამოთვლა მოსახერხებელია შემთხვევითი ცვლადის გამოყენებით. ჩავატაროთ ასეთი ექსპერიმენტი: ავაგდოთ ორჯერ მონეტა და დავითვალოთ რამდენჯერ მოვა საფასური. სამ ხდომილებას შესაძლოა ჰქონდეს ადგილი: \( A \): საფასური არც ერთხელ ამოვა; \( B \): საფასური მხოლოდ ერთხელ ამოვა; \( C \): საფასური ორჯერ ამოვა. ადვილი სანახავია, რომ $$ P(A)=0.25, \quad P(B)=0.5, […]
7. დისკრეტული შემთხვევითი ცვლადი
შესავალი წინა თავებში განვიხილეთ ალბათობის ცნება, რაც დაგვეხმარა ისეთი მოვლენების აღწერაში, რომელთა შედეგის წინასწარი განსაზღვრა შეუძლებელია (კამათლის გაგორება, ტენდერში გამარჯვების შესაძლებლობა და ა.შ.). წინამდებარე თავში კი ჩვენ გამოვიყენებთ მიღებულ ცოდნას, რათა ჩამოვაყალიბოთ ალბათური მოდელები დისკრეტული შემთხვევითი ცვლადისთვის და ვიხილოთ მათი პრაქტიკული საჭიროება სხვადასხვა ამოცანის ამოსახსნელად. სკოლის მათემატიკის კურსიდან ალბათ გახსოვთ თუ რა არის ზოგადად ცვლადი: […]
6.2. ბაიეზის წესი
წინა ქვეთავში მოყვანილი, დანადგარებზე მაგალითის გაგრძელების კუთხით, დავუშვათ, გვსურს გავიგოთ რას უდრის $ P(B_1 | A) $, ანუ თუკი შემთხვევით შერჩეული დეტალი ხარვეზიანი აღმოჩნდა, რა არის ალბათობა იმისა, რომ ის პირველმა დანადგარმა დაამზადა. როგორც ვიცით, $$ P(B_1 | A) = \frac{P(B_1 \cap A)}{P(A)}. $$ აქედან: $$ P(B_1 \cap A) = P(B_1)P(A | B_1). $$ ასევე, […]
6.1. სრული ალბათობა
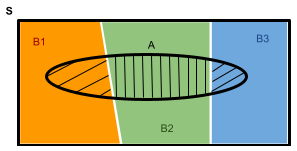
განვიხილოთ რაიმე სამი ურთიერთგამომრიცხავი და ერთობლივად ამომწურავი ხდომილება: \( B_1, B_2 \) და \( B_3 \). გავიხსენოთ, რომ “ურთიერთგამომრიცხავი” ნიშნავს იმას, რომ ამ ხდომილებებს არ გააჩნია თანაკვეთა ერთმანეთთან, ხოლო “ერთობლივად ამომწურავი” კი ნიშნავს იმას, რომ მათი გაერთიანებით მიიღება სრული სივრცე \( S \). შესაბამისად, ვენის დიაგრამების გამოყენებით, მათი გრაფიკული გამოსახვა შესაძლებელია შემდეგნაირად: გრაფიკი 6.1.1. სამი […]
6. სრული ალბათობა. ბაიეზის წესი
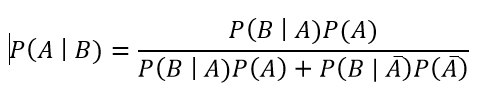
შესავალი წინამდებარე თავი შედარებით მცირე ზომის იქნება, რადგან მხოლოდ ორი ახალი რამ უნდა განვიხილოთ: სრული ალბათობა და ბაიეზის წესი. ორივე მათგანი, ძირითადად, პირობითი ალბათობის ცნებას ეფუძნება და ამიტომ, სანამ კითხვას გააგრძელებდეთ, გირჩევთ კიდევ ერთხელ კარგად გაიაზროთ პირობით ალბათობაში რას წარმოადგენს, ერთი მხრივ, პირობა და, მეორე მხრივ, ხდომილება, რომლის ალბათობასაც ვეძებთ ამ პირობით. მოვიყვანოთ მაგალითი, თუ […]
5.2. სტატისტიკური დამოუკიდებლობა
სტატისტიკური დამოუკიდებლობა წარმოადგენს კერძო შემთხვევას, რომლისთვის $ A $ ხდომილების პირობითი ალბათობა, $ B $ ხდომილების პირობით, $ A $-ს უპირობო ალბათობის ტოლია, ანუ $$ P(A|B) = P(A). $$ აღნიშნულს ადგილი აქვს მაშინ, როდესაც რაიმე ხდომილების განხორციელების ალბათობა საერთოდ არ არის დამოკიდებული სხვა ხდომილების განხორციელებაზე. ამგვარი ხდომილებების მაგალითებად შეიძლება დავასახელოთ: ვთქვათ, მოცემულია $ A $ […]
5.1. პირობითი ალბათობის ფორმულა
ვთქვათ, მოცემულია $ A $ და $ B $ ხდომილება. $ A $ ხდომილების პირობითი ალბათობა, $ B $ ხდომილების განხორციელების პირობით, აღინიშნება სიმბოლოთი $ P(A | B) $ და გამოითვლება ფორმულით $$ P(A │B)= \frac{P(A \cap B)}{P(B)}, $$სადაც $ P(B)>0. $ მაგალითი. სწრაფი კვების მომხმარებელთა $ 75\% $ სოუსად ირჩევს კეტჩუპს, $ 80\% $ […]

