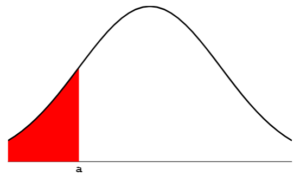
9.2. ალბათობის სიმკვრივის ფუნქცია
მიუხედავად იმისა, რომ კუმულატიური ალბათობის ფუნქციის მეშვეობით ჩვენ შეგვიძლია უწყვეტი ცვლადის ალბათობების დათვლა, ხშირად უფრო სასარგებლოა ალბათობის ამსახველი სხვა ტიპის ფუნქცია, რომელსაც ეწოდება ალბათობის სიმკვრივის

მიუხედავად იმისა, რომ კუმულატიური ალბათობის ფუნქციის მეშვეობით ჩვენ შეგვიძლია უწყვეტი ცვლადის ალბათობების დათვლა, ხშირად უფრო სასარგებლოა ალბათობის ამსახველი სხვა ტიპის ფუნქცია, რომელსაც ეწოდება ალბათობის სიმკვრივის
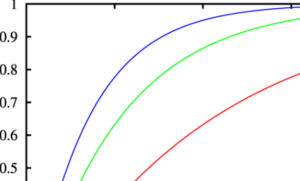
უწყვეტი შემთხვევითი ცვლადის კუმულატიური ალბათობის ფუნქცია, \( F(x) \), გამოსახავს ალბათობას იმისა, რომ \( X \) ცვლადი არ აღემატება \( x \) სიდიდეს: $$ F(x)=P(X≤x)=P(X<x)

შესავალი წინა თავებში ბევრი ვისაუბრეთ დისკრეტულ შემთხვევით ცვლადებზე. კიდევ ერთხელ ხაზი გავუსვათ, რომ შემთხვევითი ცვლადი დისკრეტული ტიპისაა, თუკი ის მნიშვნელობებს იღებს თვლადი სიმრავლიდან. სტუდენტთა რაოდენობა
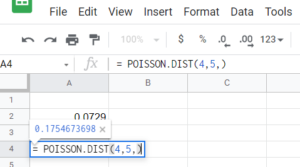
Google Sheets აღჭურვილია სპეციალური ფუნქციებით ბინომიალური, ჰიპერგეომეტრიული და პუასონის შემთხვევითი ცვლადებისთვის ალბათობების დასათვლელად. ბინომიალური ცვლადისთვის ფუნქციას აქვს შემდეგი სახე: სადაც num_successes წარმოადგენს წარმატებათა იმ რაოდენობას,

დავუშვათ, ბანკის მენეჯერი ყოველ სამუშაო დღეს აკვირდება რამდენი სასესხო განაცხადი შემოდის კლიენტებისგან და ხანგრძლივი დაკვირვების შემდეგ დაადგინა, რომ: დღის განმავლობაში შემოსული განაცხადების საშუალო რაოდენობა არ
წინა ქვეთავში განვიხილეთ მაგალითი ურნასა და ბურთებზე, სადაც საქმე გვქონდა ბინომიალურ ექსპერიმენტთან. ახლა კი წარმოვიდგინოთ, რომ ურნიდან ამოღებულ ბურთს უკან არ ვაბრუნებთ. მაშინ ცხადია, რომ